Question

Using the phythagorean theorem to find distance on a grid

Answer 1

Answer: 6.71

Step-by-step explanation

Check out the diagram below. I have added red segments to form a right triangle.

• a = 3 = vertical leg
• b = 6 = horizontal leg
• c = unknown hypotenuse = distance from point A to point B

Use the pythagorean theorem to find c.

`a^2+b^2 = c^2\\\\c = √(a^2+b^2)\\\\c = √(3^2+6^2)\\\\c = √(9+36)\\\\c = √(45)\\\\c \approx 6.708204\\\\c \approx 6.71\\\\`

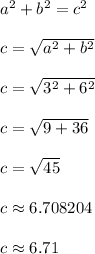
The hypotenuse is roughly 6.71 units long.

The distance from A to B is approximately 6.71 units.