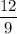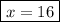Answer:

Explanation:
We can solve for x in the given right triangle by creating ratios of side lengths using the similarity property shared by all of the triangles created when dropping a right triangle's altitude (the dotted line).
First, we should solve for the short leg of the largest right triangle by applying the Pythagorean Theorem to the smallest right triangle:

where
 and
and
 are the triangle's shorter sides, and
are the triangle's shorter sides, and
 is its hypotenuse.
is its hypotenuse.
↓ plugging in the given values:
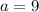 ,
,
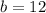

↓ simplifying the exponents on the left side

↓ executing the addition
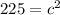
↓ taking the square root of both sides
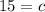
So, the short leg of the largest right triangle is 15.
Using this value, we can create the following ratios:
short leg : long leg
for the smallest triangle 9 : 12
for the middle triangle 12 :

We can solve for x by equating these ratios:

↓ multiplying both sides by

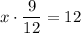
↓ multiplying both sides by