Answer:
3cosh(3x)
Explanation:
The question asks for the derivative of sinh(3x) with respect to 'x'. To solve this, we'll use the chain rule of calculus.
The hyperbolic sine function, denoted sinh(x), is defined as:
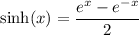
The derivative of sinh(x) with respect to 'x' is:
![(d)/(dx)[\sinh(x)]=\cosh(x)](https://img.qammunity.org/2024/formulas/mathematics/high-school/od8096j8fs6c1yes67scsb1hj1oc8ysf6m.png)
Now, to find the derivative of sinh(3x), we will make use of the chain rule. The chain rule states that if we have a function g(f(x)), then the derivative:
![\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)[f(g(x))] =f'(g(x))\cdot g'(x)\end{array}\right}](https://img.qammunity.org/2024/formulas/mathematics/high-school/h8sbxyvsty4r9839te2w2eyg23rg16kpz4.png)
Now, applying the chain rule, we get:
![\Longrightarrow (d)/(dx)[\sinh(3x)]=\cosh(3x) \cdot 3\\\\\\\\\therefore \boxed{\boxed{(d)/(dx)[\sinh(3x)]=3\cosh(3x)}}](https://img.qammunity.org/2024/formulas/mathematics/high-school/vqngkg1wfrughj35vju1px9947z850pa58.png)
So, the derivative of sinh(3x) with respect to ‘x’ is 3cosh(3x).