Question

Can answers this really quick for me i'll give 100 points

Answer 1

x = 5 and y = 4

Explanation:

Note:

When a triangle is rotated by a certain angle, such as 120°, the lengths of its sides do not change. Rotations are rigid transformations that preserve distances, angles, and shapes.

Therefore, if we rotate a triangle by 120°, the lengths of its sides will remain the same as before the rotation.

Only the positions of the vertices will change according to the rotation, while the relationships between the sides and angles will stay consistent.

`\dotfill`

For the question:

Since the length doesn't change in rotation, we can compare the side as:

`\sf x = 5 .............Equation \:1`

`\sf x+7 = 3y ......Equation \:2`

Let's solve Equation 1 for x:

From Equation 1:

`\sf x = 5`

Now, substitute the value of x into Equation 2:

`&\sf x + 7 = 3y\\\\&\sf 5 + 7 = 3y\\\\&\sf 12 = 3y`

Divide both sides by 3:

`&\sf y =(12)/(3)\\\\&\sf y = 4`

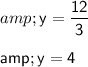
So, the solution is:

• x = 5
• y = 4