Help pleasee (3x + 2) 41

Question

asked Apr 9, 2024 129k views

2 Answers

Mohammed Zayan · Answer 1 · 2024-04-10T01:29:10+0000

Explanation:

If you observe the diagram closely, (3x+2)° and 41° are vertically opposite angles which are angles subtended between two crossing lines.

The vertically opposite angles are equal in measure.

Now equate the above and solve for x:

$3x + 2 \degree = 41 \degree$

Isolate the term containing x by subtracting 2° from both sides,

$3x = 39 \degree$

Now divide three both sides and isolate x:

$x = \large{ (39 \degree)/(3) }$

$\boxed{x = 13 \degree}$

$\therefore$ The required value of x is 13° (ans)

Y M · Answer 2 · 2024-04-14T08:22:57+0000

Answer:

x = 13

Explanation:

Note:

Vertically opposite angles are pairs of angles that are formed by the intersection of two straight lines.

When two lines intersect, they create two pairs of opposite angles that are congruent (equal) to each other.

Each pair consists of two angles, one from each of the intersecting lines, and they share a common vertex but have different rays.

$\hrulefill$

For the Question:

The given angles are vertically opposite angles.

So, it's angles are equal.

We can write it as:

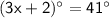
$\sf (3x+2)^\circ = 41^\circ$

Subtract 2 on both sides

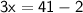
$\sf 3x = 41-2$

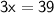
$\sf 3x = 39$

Divide both sides by 3

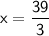
$\sf x = (39)/(3)$

$\sf x = 13$

Therefore, value of x is 13.