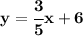Question

M=3/5, y-intercept (0,6). The equation of the line in slope-intercept form is

Answer 1

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{6})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{3}{5} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{6}=\stackrel{m}{\cfrac{3}{5}}(x-\stackrel{x_1}{0})\implies \stackrel{ \textit{slope-intercept form} }{\boxed{y=\cfrac{3}{5}x+6}}`

Answer 2

Explanation

Our task is to find the equation of the line that:

• has a slope of 3/5
• has a y-intercept at (0,6)

To write a slope-intercept equation, we need to know the values of m and b.

Bear in mind that slope-intercept is:
`\bf{y=mx+b}`.

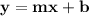M is the slope and b is the y-intercept; we have the value of the slope, it's 3/5, so, we plug that in:

• 
  `\bf{y=\cfrac{3}{5}x+b}`

For the y-intercept, we'll use the point (0,6) -> where 6 is the value of b.

Our equation is:

`\bf{y=\cfrac{3}{5}x+6}`