Question

Use the map shown below to find the distance between cities A and B to the nearest tenth.

Answer 1

7.8

Explanation:

If you understand the method I'm about to lay out for this simple one, then you'll be able to do your subway and zipline questions. Those just have more line segments to work with. (But start with the subway one first.)

Imagine line segment AB as the hypotenuse of a right triangle. Draw a line from B over to the y-axis. Then from there draw down the y-axis to A, which is at (0,0). Do you have it, or see it? You should have an upside-down right triangle that starts at (0,0), goes up to (0,6), over to (5,6), and then back to A at (0,0).

Now you apply the Pythagorean Theorem:

`a^(2) + b^(2) = c^(2)`

'c' IS ALWAYS THE HYPOTENUSE, don't forget that. 'a' and 'b' are the two other sides, and it doesn't matter which you call which.

But let's call 'a' the segment from A up to (0,6). How long is it? It's 6, right? 6 units straight up the y-axis.

Then 'b' is the segment from (0,6) over to B, which is at (5,6). How long is that one? It's 5 units right? Parallel to the x-axis from 0 over to 5.

So now just plug 6 and 5 in for a and b:

`6^(2) + 5^(2) = x^(2)`

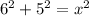
Simplify to:
`36 +25 = c^(2)`

Or:
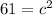`61 = c^(2)` Turn that around to:
`c^(2) = 61`

And then you can see that whatever c is, when you square it you have to get 61.

So take the square root of both sides to get:

`c = √(61) = 7.8`

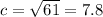
You can do that with your subway problem in 2 steps and add the distances together. OR SINCE THAT ONE IS A STRAIGHT LINE, you can use the starting and ending points and run the "sides" of the triangle vertically and horizontally until they intersect, and that's your right triangle, then find the length of its hypotenuse.

The zip line one is just many iterations of this distance-between-cities problem. Tedious, but just work each triangle one at a time.