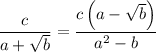Question

How do you rationalise the denominator of a surd with denominator a + √b?

Answer 1

`\displaystyle{(c)/(a+√(b)) = (c\left(a-√(b)\right))/(a^2-b)}`

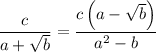
Explanation:

Hi! Suppose you are looking to rationalize the expression with the denominator in the form of a + √b.

Let's look into the following sample expression:

`\displaystyle{(c)/(a+√(b))`

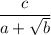
Here, we see that the denominator is not rationalized because it contains a surd. To rationalize this kind of denominator, we have to make sure that the surds are not there in the denominator. We have learned that if we want to rationalize a simple surd, we multiply by the surd itself for both the numerator and denominator.

However, that does not apply to this case. If we multiply both the numerator and denominator by the radical expression, this happens:

`\displaystyle{(c)/(a+√(b)) \Rightarrow (c \left(a+√(b)\right))/(\left(a+√(b)\right)\left(a+√(b)\right)) \Rightarrow (c\left(a+√(b)\right))/(\left(a+√(b)\right)^2) \Rightarrow (c\left(a+√(b)\right))/(a^2+2a√(b)+b) }\\\\\displaystyle{\text{Note that} \ \left(x+y)^2=x^2+2xy+y^2}`

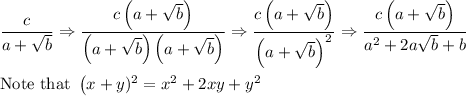
See how the surd is still there in the denominator, not only that but it also makes the expression even more complicated. In order to rationalize this case of the surd expression, we have to apply the difference of two squares:

`\displaystyle{\left(x+y\right)\left(x-y\right)=x^2-y^2}`

So instead of multiplying by the radical expression itself, we multiply its conjugate, the opposite operator.

`\displaystyle{(c)/(a+√(b)) \Rightarrow (c \left(a-√(b) \right))/(\left(a+√(b)\right) \left(a-√(b)\right) ) \Rightarrow (c\left(a-√(b)\right))/(a^2-\left(√(b)\right)^2)\Rightarrow (c\left(a-√(b)\right))/(a^2-b) \ \ \#}`

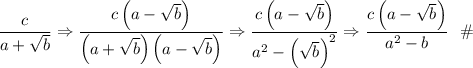
As you see, there are no surds left now and the final expression is also equal to the initial expression. Therefore, we can conclude that:

`\displaystyle{(c)/(a+√(b)) = (c\left(a-√(b)\right))/(a^2-b)}`