Question

Choose an equivalent expression for

Answer 1

In order to find the equivalent expression for
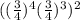`(( (3)/(4)) {}^(4) ( (3)/(4)) {}^(3)) {}^(2)` , we will solve among the brackets.

Firstly,we will solve the exponents inside of the brackets,

for that, we will add the exponents as their bases are same

`\rightarrow \: (( (3)/(4)) {}^(4) ( (3)/(4)) {}^(3)) {}^(2) = ( ( (3)/(4)) {}^(4 + 3)) {}^(2)`

`\rightarrow \: ( ( (3)/(4)) {}^(7)) {}^(2)`

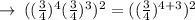
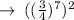
Now , we will multiply among the exponents in and out of the brackets

`\rightarrow \: ( (3)/(4)) {}^(7 * 2)`

`\rightarrow \: ( (3)/(4)) {}^(14)`

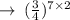
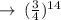
Therefore, option (4)
`\: ( (3)/(4)) {}^(14)` is our answer .

Answer 2

`\left((3)/(4)\right)^(14)`

Explanation:

`\boxed{\begin{aligned} &\textsf{ The laws of exponents with whole number exponents are:} \\\\& \textsf{ Product rule: } \sf (a^m)(a^n) = a^((m+n) )\\\\&\textsf{ Quotient rule: } \sf ( (a^m))/((a^n)) = a^((m-n) )\\\\& \textsf{ Power rule: } \sf (a^m)^n = a^((mn))\\\\& \textsf{ Zeroth power rule: } \sf a^0 = 1\\\\& \textsf{ Negative power rule: } \sf a^(-n) = (1)/(a^n )\end{aligned}}`

Let's apply these laws to the expression.

`\sf \left[\left((3)/(4)\right)^4\left((3)/(4)\right)^3\right]^2`

The first step is to use the product rule:

`\sf \left[\left((3)/(4)\right)^4\left((3)/(4)\right)^3\right]^2 = \left[\left((3)/(4)\right)^(4+3)\right]^2 = \left[\left((3)/(4)\right)^(7)\right]^2`

The second step is to use the power rule:

`\sf \left[\left((3)/(4)\right)^(7)\right]^2 = \left((3)/(4)\right)^(7* 2) = \left((3)/(4)\right)^(14)`

`\textsf{ Therefore, the simplified expression is : }\left((3)/(4)\right)^(14)`