Answer:
22 sq. units.
Explanation:
To Find:
Solution:
Given,
Coordinates of point H (7, -4)
Coordinates of point J (-4, -4)
Coordinates of point I (7, -8)
Also, from the given diagram it can be inferred that it is a right-angled triangle.
Here,
Length of side HJ is = 7 units + 4 units = 11 units [Base]
Length of side HI is = 8 units - 4 units = 4 units [Height]
So,
By Pythagoras Theorem, length of side JI is,
=
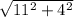
=
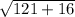
=
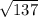 = 11.7 (approx.) units [Hypotenuse]
= 11.7 (approx.) units [Hypotenuse]
Then,
Area of the triangle HIJ will be,
=
 × Base × Height
× Base × Height
=
 × 11 units × 4 units
× 11 units × 4 units
= 22 sq. units
Hence,
The required area of the triangle is 22 sq. units. (Ans)