Question

Write an equation for the function graphed below using the point (pi/6,7)​

Answer 1

Midline: y = 5

Amplitude: 2

Period: π

B = 2

`\textsf{Equation:}\quad y=2\cos\left(2\left(x-(\pi)/(6)\right)\right)+5`

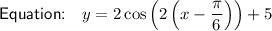
Explanation:

Midline

The midline of a sinusoidal graph is the horizontal line around which the sinusoidal curve oscillates. It is the midpoint between the maximum and minimum values of the graph, and corresponds to the vertical shift of the function from its parent function.

From inspection of the graph, the midline is y = 5.

`\hrulefill`

Amplitude

The amplitude is the vertical distance between the function's minimum or maximum point and its midline.

From inspection of the graph, the maximum y-value of the function is y = 7. Therefore, as its midline is y = 5, the amplitude is:

`A = |7 - 5| = \boxed{2}`

`\hrulefill`

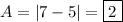
Period

The period is the horizontal length of one cycle of the curve

From inspection of the graph, the period is π.

`\hrulefill`

Value of B

As period = 2π/B, then the value of B is:

`(2\pi)/(B)=\pi\implies\frac{2\pi}\pi}=B\implies \boxed{B=2}`

`\hrulefill`

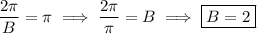
Equation

The standard form of a cosine function is:

`\boxed{f(x)=A\cos(B(x+C))+D}`

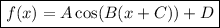
where:

• |A| = amplitude (height from the midline to the peak).
• 2π/B = period (horizontal length of one cycle of the curve).
• C = phase shift (horizontal shift - positive is to the left).
• D = vertical shift.

The parent cosine function passes through (0, 1). Therefore, if the graphed function passes through (π/6, 7), it has shifted π/6 units to the right, so C = -π/6.

Therefore, the values of A, B, C and D are:

• A = 2
• B = 2
• C = -π/6
• D = 5

Substitute the values into the standard equation:

`y=2\cos\left(2\left(x-(\pi)/(6)\right)\right)+5`