Question

It is given that V is directly proportional to r³, when r =4, V = 32.

(a) find the equation connecting r and V.
(b) hence, find
(I) the value of V when r = 5,
(Ii) the value of r when V = 108

Answer 1

Explanation:

`v \alpha {r}^(3) \\ v = k {r}^(3)`

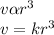
where k is the constant of proportionality

so to find the constant k we first make k the subject of the relation.

`k = \frac{v}{ {r}^(3) }`

where r is 4 and v is 32

`k = \frac{32}{ {4}^(3) } \\ k = 0.5`

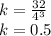
now to find the value of v when r is 5.

`v = 0.5( {5})^(3) = 62.5`

now to find the value of r when v is equal to 108. yeah we need to make r the subjects of the relation

`r = \sqrt[3]{ (v)/(0.5) }`

`r = \sqrt[3]{ (108)/(0.5) } = 6`