Question

recall the equation for a circle with center (h,k) and radius r. At what point in the first quadrant does the line with equation y = 1.5x + 3 intersect the circle with radius 6 and center (0,3)

Answer 1

`\textsf{Exact point of intersection:}\quad \left((12√(13))/(13),(39+18√(13))/(13)\right)`

`\textsf{Rounded point of intersection:} \quad (3.328, 7.992)`

Explanation:

The equation of a circle is given by:

`\large\boxed{(x - h)^2 + (y - k)^2 = r^2}`

where:

• (h, k) is the center.
• r is the radius.

To find the point(s) of intersection of the line y = 1.5x + 3 and a circle with a center with radius 6 and center (0, 3), substitute the following values into the equation of a circle formula:

• h = 0
• k = 3
• r = 6
• y = 1.5x + 3

Therefore:

`(x - 0)^2 + (1.5x + 3 - 3)^2 = 6^2`

Solve for x:

`\begin{aligned}(x - 0)^2 + (1.5x + 3 - 3)^2&= 6^2\\\\x^2+(1.5x)^2&=36\\\\x^2+2.25x^2&=36\\\\3.25x^2&=36\\\\(13)/(4)x^2&=36\\\\x^2&=(144)/(13)\\\\x&=\pm \sqrt{(144)/(13)\\\\x&=\pm(12)/(√(13)\\\\x&=\pm(12√(13))/(13))\end{aligned}`

As the point is in the first quadrant, we take the positive value of x only:

`x=(12√(13))/(13)`

To find the y-coordinate of the point, substitute the found value of x into the equation of the line and solve for y:

`\begin{aligned}y&=1.5\left((12√(13))/(13)\right)+3\\\\y&=(3)/(2)\left((12√(13))/(13)\right)+3\\\\y&=(36√(13))/(26)+3\\\\y&=(18√(13))/(13)+(39)/(13)\\\\y&=(39+18√(13))/(13)\end{aligned}`

Therefore, the point of intersection of the line y = 1.5x + 3 and the circle with center (0, 3) and radius 6 in the first quadrant is exactly:

`\left((12√(13))/(13),(39+18√(13))/(13)\right)`

If we round the coordinates to the nearest thousandth (3 decimal places), we get:

`(3.328, 7.992)`

Answer 2

The point in the first quadrant is (3.33, 7.995).

Explanation:

The equation for a circle with center (h, k) and radius r is:

`\sf (x - h)^2 + (y - k)^2 = r^2`

In this case, the center of the circle is (0, 3) and the radius is 6.

So the equation of the circle is:

`\sf (x - 0)^2 + (y - 3)^2 = 6^2`

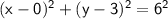
We can rewrite this equation as:

`\sf x^2 + y^2 - 6y +9 = 36`

`\sf x^2 + y^2 - 6y = 36-9`

`\sf x^2 + y^2 - 6y = 27`

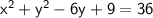
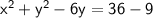
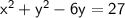
The line with equation y = 1.5x + 3 intersects the circle when the two equations are equal.

So we can substitute y = 1.5x + 3 into the equation for the circle to get:

`\sf x^2 + (1.5x + 3)^2 - 6(1.5x + 3) = 27`

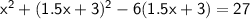
Expand the square term:

`\sf x^2 + 2.25x^2 + 9x + 9 - 6(1.5x + 3) = 27`

Distribute the constant term 6 on the right side of the equation:

`\sf x^2 + 2.25x^2 + 9x + 9 - 9x -18 = 27`

Combine like terms:

`\sf \sf 3.25x^2 -9+9 = 27+9`

`\sf 3.25x^2 = 36`

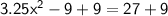
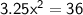
Divide both sides by 3.25:

`\sf x^2 =(36)/(3.25)`

Take the square root of both sides:

`\sf x =\sqrt{(36)/(3.25)}`

`\sf x \approx \pm 3.33`

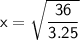
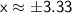
Since we're looking for the point in the first quadrant, take the positive square root:

`\sf x \approx 3.33`

Now substitute the x value back into the line equation to find the corresponding y value:

`\sf y = 1.5* (3.33) + 3`

`\sf y \approx 4.995 + 3`

`\sf y \approx 7.995`

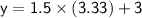
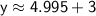
So, the point of intersection between the line(y = 1.5x + 3 and the circle with center (0, 3)and radius 6 in the first quadrant is approximately (3.33, 7.995).