Question

Please answer and explain the link below

Answer 1

2

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Distributive Property

Algebra I

• Terms/Coefficients
• Functions
• Function Notation

Calculus

Limits

Limit Rule [Constant]:
`\displaystyle \lim_(x \to c) b = b`

Definition of a Derivative:
`\displaystyle f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)`

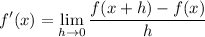
Explanation:

Step 1: Define

Identify

f(x) = 2x - 5

Step 2: Differentiate

1. [Limit] Substitute in x [Function f(x)]:
   `\displaystyle \lim_(\triangle x \to 0) ([2(x + \triangle x) + 5] - f(x))/(\triangle x)`
2. [Limit] Substitute in function:
   `\displaystyle \lim_(\triangle x \to 0) ([2(x + \triangle x) + 5] - (2x + 5))/(\triangle x)`
3. [Distributive Property] Distribute 2:
   `\displaystyle \lim_(\triangle x \to 0) ([2x + 2\triangle x + 5] - (2x + 5))/(\triangle x)`
4. [Distributive Property] Distribute negative:
   `\displaystyle \lim_(\triangle x \to 0) (2x + 2\triangle x + 5 - 2x - 5)/(\triangle x)`
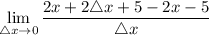
5. [Subtraction] Combine like terms:
   `\displaystyle \lim_(\triangle x \to 0) (2\triangle x)/(\triangle x)`
6. [Division] Simplify:
   `\displaystyle \lim_(\triangle x \to 0) 2`
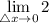
7. Evaluate limit [Limit Rule - Constant]:
   `\displaystyle 2`

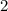
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e