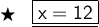Question

Angles A and B are complementary to each other. If m∠A = 37° and m∠B = (3x + 17)°, find the value of x.

Answer 1

Explanation:

Complementary angles add upto 90°. Angles A and B are complementary to each other. Measures of ∠A and ∠B is provided in the question. With this data, let's form an equation:

`m∠A + m∠B = 90°`

Substituting values,

`37° + 3x + 17° = 90°`

Now solving the equation,

`3x + 54° = 90°`

`3x = 36°`

`x = 12°`

~The required value of x is 12° (ans)

Answer 2

Answer: The value of x is 12.

Explanation:

Our task is to solve for x.

We're given the following angles:

• ∠A = 37°
• ∠B = (3x + 17)°

We're also given that these two angles are complementary to each other.

If two angles are complementary to each other, it means that they add up to 90°. Therefore,

`\sf{m\angle A + m\angle B = 90^o}`

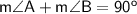
We know the measures of each of these angles.

`\sf{37+3x+17=90}`

Combine like terms:

`\sf{54+3x=90}`

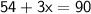
Subtract 54 from both sides:

`\sf{3x=36}`

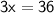
Divide both sides by 3.

`\bigstar\phantom{12}\underline{\large\boxed{\sf{x=12}}}`