Question

The graph of (x+3)²/9 + y²/25=1

is an ellipse.

Part I: The standard form equation of an ellipse that is not centered at the origin is

(x-h)²/ a² + (y-v)²/ h² =1

A. Find the center (h, v) of the ellipse with the given equation.

Answer 1

Centre of the elipse lies at (-3,0)

Explanation:

The standard form equation of an ellipse that is not centered at the origin is given as,

`\frac{(x - h) {}^(2) }{ {a}^(2) } + \frac{(y - v) {}^(2) }{ {b}^(2) } = 1`

where centre is at (h,v) and horizontal axis has a length of 2a and vertical axis has a length of 2b.

Given, the graph of an elipse:

`\frac{(x + 3) {}^(2) }{9} + \frac{y {}^(2) }{25} = 1`

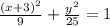
If we arrange this equation in such a way to resemble the standard form, we can identify the values of h, v, a and b.

`\frac{((x - ( - 3)) {}^(2) }{ {3}^(2) } + \frac{(y - 0) {}^(2) }{5 {}^(2) }`

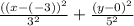
From here we can conclude: h = -3 and v = 0. Therefore, the centre of the given elipse lies at (-3,0)