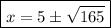Question

Factor x^2-10x-140=0

Answer 1

`x = 5 \pm √(165)`

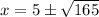
Explanation:

We can attempt to solve for x in the quadratic equation:

`x^2 - 10x - 140 = 0`

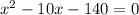
by factoring.

We can factor using the rule:

`\text{If } x^2 + cx + d = (x + a)(x + b), \text{ then } a + b = c \text{ and } a \cdot b = d.`

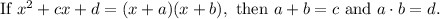
First, we can assign the following variable values from the given equation:

• 
  `c = -10`
• 
  `d = -140`

We know that
`a` and
`b` must multiply to -140, we can list out -140's factor pairs. The numbers in the pair whose factors add to -10 are
`a` and
`b`.

• -140, 1
• -70, 2
• -35, 4
• -28, 5
• -20, 7
• -10, 14

We can see that none of these factor pairs add to -10; therefore the equation is not factorable.

So, we can solve for x by completing the square:

`x^2 - 10x - 140 = 0`

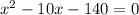
↓ adding 140 to both sides

`x^2 - 10x = 140`

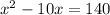
↓ adding (-10/2)² to both sides (which simplifies to (-5)², then to 25)

`x^2 -10x + 25 = 140 + 25`

↓ factoring the left side as a perfect square

`(x-5)^2 = 165`

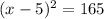
↓ taking the square root of both sides

`x-5 = \pm√(165)`

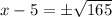
↓ adding 5 to both sides

`\boxed{x = 5 \pm √(165)}`