Question

How can you rewrite 5^-6/5^-4?

Answer 1

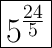`\huge\boxed{5^{(24)/(5)}}` OR
`\huge\boxed{\left(\sqrt[5]{5}\right)^(\!24)}`

Explanation:

We can rewrite the exponential expression:

`\left(5^{-\!(6)/(5)} \right)^(\!-4)`

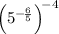
using the power of a power rule, which states that:

`(x^a)^b = x^(a\,\cdot \,b)`

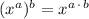
Using this rule, the expression becomes:

`5^{\left(\!-\!(6)/(5) \,\cdot \,(-4) \right)}`

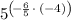
This can be simplified further by executing the multiplication within the exponent:

`\huge\boxed{5^{(24)/(5)}}`

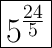
Note that this can also be rewritten by converting the fractional exponent to a radical:

`\huge\boxed{\left(\sqrt[5]{5}\right)^(\!24)}`