Question

How many solutions does the system have

Answer 1

1 solution

Explanation:

A solution to a system of equations is a point where the equations intersect — in other words, where their x and y values are the same.

In the given system:

`\begin{cases} y=-x+5 \\ y=3x+5 \end{cases}`

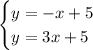
we can see that both equations are written in slope-intercept form:

`y=mx+b`

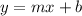
where
`m` is the slope of the line and
`b` is the y-intercept.

We can see that both equations have a y-intercept at 5; therefore, the solution to the system is at (0, 5).

We can deduce that there are no other solutions because the lines have different slopes; therefore, they will not intersect at any other point.

So, the system of equations

`\begin{cases} y=-x+5 \\ y=3x+5 \end{cases}`

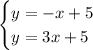
has 1 solution.