Answer:
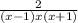 ,
,
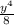 , and
, and
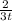
Explanation:
1.
Let's find a common denominator:
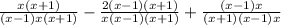
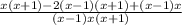
=
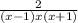
2/(x-1)x(x+1)
2.
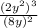
Distribute exponents:
2^3(y^2)^3
__________
8^2(y)^2
Numerator:
2 to the power of 3 equals (2 · 2 · 2) = 8
y to the power of 2 to the power of 3 equals, y to the power of 6 (this is because when exponents in parenthesis are held to the power of another number outside of the parenthesis, you multiply them)
Now let's simplify the denominator:
8 to the power of 2 equals (8 · 8) = 64
y to the power of 2 is just y to the power of 2, so our new expression is:
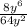
Let's cancel the terms further:
8/64 can be simplified to 1/8
And when you cancel exponents, you subtract the denominator's exponent from the numerator's exponent (
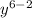 =
=
 )
)
Now put them together:

Which is,
=
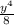
y^4/8
3.
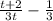
The common denominator for both fractions is 3t, so let's make -1/3's denominator 3t by multiplying t to both the numerator and the denominator:
-1 · t
_____ = -1(t)/3t = -t/3t
3 · t
Now let's solve for the numerator:
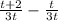
(t + 2) - t, the t's cancel out, t - t + 2 = 2
And the denominator stays the same, so it will still equal 3t
Finally, you'll get an answer of
=
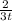
2/3^2