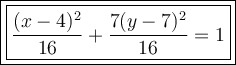Question

Find an equation in standard form for the ellipse with center at (4,7), horizontal major axis of length 8 and passes through the point (7,6).

Answer 1

`((x-4)^2)/(16)+(7(y-7)^2)/(16)=1`

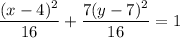
Explanation:

The major axis of an ellipse is the longest line segment that can be drawn within the ellipse. It passes through the center of the ellipse and its endpoints lie on the ellipse's boundary.

The standard equation of an ellipse with a horizontal major axis is:

`\large\boxed{((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1}`

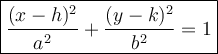
where:

• 2a is the major axis.
• 2b is the minor axis.
• (h, k) is the center.
• (h±a, k) are the vertices.
• (h, k±b) are the co-vertices.
• (h±c, k) are the foci, where c² = a² - b².

Given the center of the ellipse is (4, 7):

• 
  `h = 4`
• 
  `k = 7`

Given the major axis is 8:

`2a=8 \implies a=4`

Substitute the found values of h, k and a into the standard equation:

`((x-4)^2)/(4^2)+((y-7)^2)/(b^2)=1`

`((x-4)^2)/(16)+((y-7)^2)/(b^2)=1`

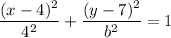
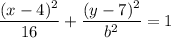
Given the ellipse passes through the point (7, 6), substitute x = 7 and y = 6 into the equation and solve for b²:

`\begin{aligned}((7-4)^2)/(16)+((6-7)^2)/(b^2)&=1\\\\((3)^2)/(16)+((-1)^2)/(b^2)&=1\\\\(9)/(16)+(1)/(b^2)&=1\\\\(1)/(b^2)&=1-(9)/(16)\\\\(1)/(b^2)&=(16)/(16)-(9)/(16)\\\\(1)/(b^2)&=(7)/(16)\\\\16&=7b^2\\\\b^2&=(16)/(7)\end{aligned}`

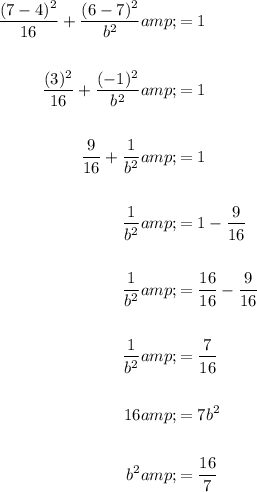
Substitute the found value of b² into the equation:

`((x-4)^2)/(16)+((y-7)^2)/((16)/(7))=1`

`((x-4)^2)/(16)+(7(y-7)^2)/(16)=1`

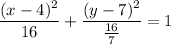
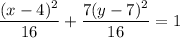
Therefore, the equation in standard form for the ellipse with center at (4, 7), horizontal major axis of length 8, and passes through the point (7, 6) is:

`\large\boxed{\boxed{((x-4)^2)/(16)+(7(y-7)^2)/(16)=1}}`