Question

Find all solutions to the equation r(r+4)=8.

Answer 1

r(r+4)=8.

r²+4r-8=0

a=1; b=4; c=-8

b²-4ac =4²-4(1*-8)= 16+32=48

Discriminant of the trinomial: Δ=b²−4ac=48

Root of the discriminant: √Δ=4√3

The discriminant Δ is strictly positive, the equation x²+4x−8=0

admits two solutions.

solution 1 =(-b-√Δ)/2 =(-4-4√3)/2 = -2-2√3

solution 2 = (-b+√Δ)/2a = (-4+4√3)/2 = -2+2√3

Explanation:

Answer 2

Hello!

Answer:

`\Large \boxed{\sf x =-2 \pm 2√(3) }}`

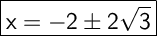
Explanation:

→ We want to solve this equation:

`\sf r(r+4)=8`

◼ Simplify the left side:

`\sf r^2+4r=8`

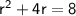
◼ Bring the equation back to 0:

`\sf r^2+4r-8=0`

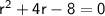
→ It's a quadratic equation because it's on the form ax² + bx + c = 0.

→ To solve a quadratic equation, we have the quadatic formula:

`\sf x = (-b \pm √(b^2 - 4ac) )/(2a)`

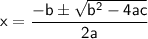
In our equation:

`\sf a = 1\\b = 4\\c = -8`

◼ Let's apply the quadratic formula:

`\sf x = (-4 \pm √(4^2 - 4(1)(-8)) )/(2(1))`

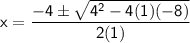
◼ Simplify the left side:

`\sf x = (-4 \pm √(48) )/(2)`

`\sf x = \frac{-4 \pm \sqrt{2*2*√(3) } }{2}`

`\sf x = \frac{-4 \pm 4√(3) } {2}`

`\boxed{\sf x =-2 \pm 2√(3) }}`

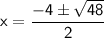
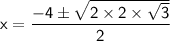
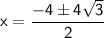
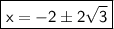
Conclusion:

The solution of the equation r(r+4) = 8 is -2±2√3.