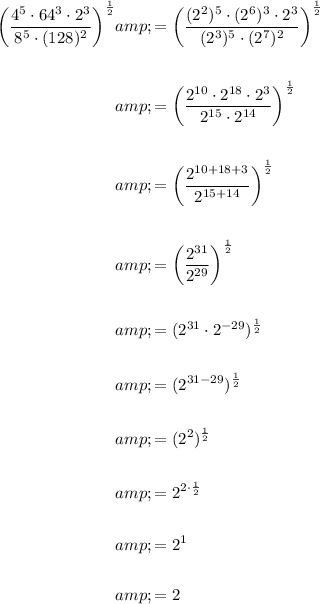Question

Can anyone help me this……

Answer 1

See below for proof.

Explanation:

Given equation:

`\left((4^5\cdot64^3\cdot2^3)/(8^5\cdot(128)^2)\right)^{(1)/(2)}=2`

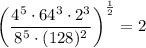
To prove the given equation, use the laws of exponents to combine like terms and simplify.

`\boxed{\begin{array}{rl}\underline{\sf Laws\;of\;Exponents}\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Negative\;Exponent:&a^(-m)=(1)/(a^m)\\\\\end{array}}`

Begin by rewriting all the bases using prime factorization:

`4=2^2`

`64=2^6`

`8=2^3`

`128=2^7`

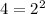
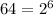
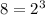
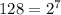
Therefore:

`\left((4^5\cdot64^3\cdot2^3)/(8^5\cdot(128)^2)\right)^{(1)/(2)}=\left(((2^2)^5\cdot(2^6)^3\cdot2^3)/((2^3)^5\cdot(2^7)^2)\right)^{(1)/(2)}`

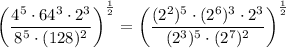
Apply the power of a power rule:

`=\left((2^(10)\cdot2^(18)\cdot2^3)/(2^(15)\cdot2^(14))\right)^{(1)/(2)}`

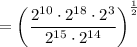
Now all the bases are the same, apply the product rule:

`\begin{aligned}&=\left((2^(10+18+3))/(2^(15+14))\right)^{(1)/(2)}\\\\&=\left((2^(31))/(2^(29))\right)^{(1)/(2)}\end{aligned}`

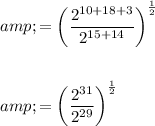
Apply the negative exponent rule to bring 2²⁹ to the numerator:

`=\left(2^(31) \cdot 2^(-29)\right)^{(1)/(2)}`

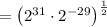
Apply the product rule:

`\begin{aligned}&=\left(2^(31-29)\right)^{(1)/(2)}\\\\&=\left(2^(2)\right)^{(1)/(2)}\end{aligned}`

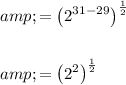
Finally, apply the power of a power rule:

`\begin{aligned}&=2^{2\cdot(1)/(2)}\\\\&=2^(1)\end{aligned}`

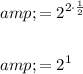
As a¹ = a, then:

`=2`

Hence, we have proved that:

`\left((4^5\cdot64^3\cdot2^3)/(8^5\cdot(128)^2)\right)^{(1)/(2)}=2`

`\hrulefill`

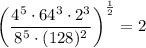
As one calculation:

`\begin{aligned}\left((4^5\cdot64^3\cdot2^3)/(8^5\cdot(128)^2)\right)^(\frac12)&=\left(((2^2)^5\cdot(2^6)^3\cdot2^3)/((2^3)^5\cdot(2^7)^2)\right)^(\frac12)\\\\&=\left((2^(10)\cdot2^(18)\cdot2^3)/(2^(15)\cdot2^(14))\right)^(\frac12)\\\\&=\left((2^(10+18+3))/(2^(15+14))\right)^(\frac12)\\\\&=\left((2^(31))/(2^(29))\right)^(\frac12)\\\\&=(2^(31)\cdot 2^(-29))^(\frac12)\\\\&=(2^(31-29))^{(1)/(2)}\\\\&=(2^(2))^(\frac12)\\\\&=2^(2\cdot\frac12)\\\\&=2^(1)\\\\&=2\end{aligned}`