The change in internal energy
 of the gas during the process is
of the gas during the process is
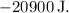
To find the heat added to or taken from the gas during its expansion, we can use the first law of thermodynamics, which states:
![\[ \Delta U = Q - W \]](https://img.qammunity.org/2024/formulas/physics/high-school/8qa3gbsguqxy9xizzvudr1zqhjtldcju8j.png)
Where:
-
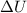 is the change in internal energy of the gas.
is the change in internal energy of the gas.
-
 is the heat added to or taken from the gas.
is the heat added to or taken from the gas.
-
 is the work done by the gas.
is the work done by the gas.
Given that the gas expands at a constant pressure of 110 kPa from an initial volume of 0.77 m³ to a final volume of 0.96 m³, the work done by the gas during expansion
 can be calculated using the formula:
can be calculated using the formula:
![\[ W = P \cdot \Delta V \]](https://img.qammunity.org/2024/formulas/physics/high-school/79gtso4p6su9fehcmd2vcktht21jk1lavo.png)
Where:
- P is the pressure (110 kPa).
-

Given:
-
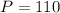 kPa
kPa
-
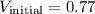 m³
m³
-
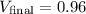 m³
m³
![\[ \Delta V = V_{\text{final}} - V_{\text{initial}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/a15rgr9vo67b7novjho975vrmwi08ubvew.png)
![\[ = 0.96 \, \text{m³} - 0.77 \]](https://img.qammunity.org/2024/formulas/physics/high-school/eoakjtm1jkv24tkhmksyyj0wz94q9hevcy.png) m³
m³
Now, let's calculate the work done by the gas:
![\[ W = P \cdot \Delta V = 110 \, \text{kPa} * 0.19 \, \text{m³} \]](https://img.qammunity.org/2024/formulas/physics/high-school/on3vzvmjlt395y32cdrh5wylxkqhzuafl7.png)
To perform the calculation, let's convert kPa to Pa (1 kPa = 1000 Pa):
![\[ W = 110 * 10^3 \, \text{Pa} * 0.19 \, \text{m³} = 20900 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/high-school/lb6ozpnmu2htcpufhyvktsnq0lk83sem04.png)
The work done by the gas during expansion is
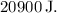
Now, using the first law of thermodynamics:
![\[ \Delta U = Q - W \]](https://img.qammunity.org/2024/formulas/physics/high-school/8qa3gbsguqxy9xizzvudr1zqhjtldcju8j.png)
Since the process is adiabatic (no heat exchange), Q = 0. Therefore:
![\[ \Delta U = -W = -20900 \, \text{J} \]](https://img.qammunity.org/2024/formulas/physics/high-school/hkni9869w8to3y3iik7pw0qobxy7v1pkfp.png)