Thus, the solution for θ in the given range

To solve the trigonometric equation
 we'll follow these steps:
we'll follow these steps:
1. Express in terms of sine and cosine: Convert secant and cosecant to their equivalent in terms of sine and cosine.
![\[ \sec(x) = (1)/(\cos(x)) \quad \text{and} \quad \csc(x) = (1)/(\sin(x)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/taliltju385wrbc45nzacblhog87fgccsd.png)
2. Rewrite the equation: Substitute the expressions for secant and cosecant.
3. Manipulate the equation: Try to simplify and solve for

4. Consider the domain: Ensure the solutions are within
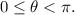
Let's start solving it step by step.
Step 1: Express in Terms of Sine and Cosine
![\[(1)/(\cos(-2\theta + (2\pi)/(5))) = (1)/(\sin(-2\theta + (33\pi)/(10)))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xtkpsaqcj91s4n5n6q8tu6t0ml0r1oinyu.png)
Step 2: Rewrite the Equation
![\[\sin(-2\theta + (33\pi)/(10)) = \cos(-2\theta + (2\pi)/(5))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zcrs0h0l4q9mdk0u03w66ppvac6akqq9k2.png)
Step 3: Manipulate the Equation
Use the identity
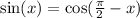 to rewrite the sine term as a cosine:
to rewrite the sine term as a cosine:
![\[\cos((\pi)/(2) - (-2\theta + (33\pi)/(10))) = \cos(-2\theta + (2\pi)/(5))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hq7za0o5few06q47tee0n1qvt8a3ymwl95.png)
Simplify both sides:
![\[\cos(2\theta - (23\pi)/(10)) = \cos(-2\theta + (2\pi)/(5))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e2cbto8tt44oqjp7d25k5axw06lld2gf9l.png)
Step 4: Solve for θ
For
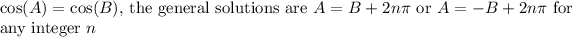 . Apply this to our equation:
. Apply this to our equation:
![\[2\theta - (23\pi)/(10) = -2\theta + (2\pi)/(5) + 2n\pi \quad \text{or} \quad 2\theta - (23\pi)/(10) = 2\theta - (2\pi)/(5) + 2n\pi\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hp1g6fxfzblm91b3969vgz1nvwutyssubk.png)
Solving these equations will give us the values of
 in the given domain. Let's calculate these solutions.
in the given domain. Let's calculate these solutions.
After solving the equations, we find the following:
1. For the first equation, the solution is
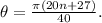
2. The second equation does not yield any additional solutions.
Since we are interested in solutions where
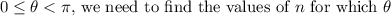 falls within this range.
falls within this range.
Let's calculate these specific values for n and the corresponding values of

The valid values of
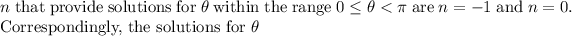 are:
are:
1. For
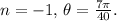
2. For

These are the solutions for the given trigonometric equation within the specified domain.