Question

if $1200 are deposited into an account with an 11% interest rate, compounded monthly, what is the balance after 11 years?

Answer 1

`~~~~~~ \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{original amount deposited}\dotfill &\$1200\\ r=rate\to 11\%\to (11)/(100)\dotfill &0.11\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{monthly, thus twelve} \end{array}\dotfill &12\\ t=years\dotfill &11 \end{cases}`

`A = 1200\left(1+(0.11)/(12)\right)^(12\cdot 11) \implies A = 1200( 1.0091\overline{66})^(132)\implies A \approx 4002.06`

Answer 2

Balance after 11 years is $4002.06

Explanation:

The interest is compounded monthly, which means that the interest is calculated and added to the account every month. This means that the interest earned in each month is based on the balance in the account at the beginning of the month, plus the interest earned in the previous month.

The formula for compound interest is:

`\sf A = P * \left(1 + (r)/(n)\right)^(nt)`

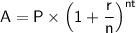
where:

• A is the final amount (balance) after t years.
• P is the initial principal amount (initial deposit), which is $1200 in this case.
• r is the annual interest rate (as a decimal), which is 11% or 0.11 in this case.
• n is the number of times the interest is compounded per year, which is monthly compounding, so n=12.
• t is the number of years, which is 11 in this case.

Plugging in the values:

`\sf A = 1200 * \left(1 + (0.11)/(12)\right)^(12 * 11)`

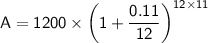
Calculating the value within the parentheses:

• 
  `\sf \left(1 + (0.11)/(12)\right) \approx 1.009166667`

Calculating the exponent:

• 
  `\sf 12 * 11 = 132`

Now we can plug these values back into the formula:

`\sf A = 1200 * \left(1.009166667\right)^(132)`

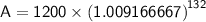
Calculating A.

`\sf A \approx 1200 * 3.335050662`

`\sf A \approx 4002.060774`

`\sf A \approx 4002.06 \textsf{ in d.p}`

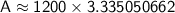
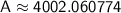
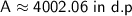
So, after 11 years, the balance in the account will be approximately $4002.06