Question

Find the amount of a continuous money flow in which $175 per year is being invested at 7.5%, compounded continuously for 20 years.

Answer 1

To find the amount of a continuous money flow in which $175 per year is being invested at 7.5%, compounded continuously for 20 years, we can use the formula for compound interest.

Step-by-step explanation:

To find the amount of a continuous money flow, we can use the formula for compound interest:

A = P * e^(rt)

Where:

• A is the final amount
• P is the principal amount (initial investment)
• e is the base of the natural logarithm (approximately 2.71828)
• r is the interest rate
• t is the time in years

Given that $175 is being invested at 7.5% compounded continuously for 20 years, we can plug in the values:

A = $175 * e^(0.075 * 20)

A ≈ $614.45

Therefore, the amount of the continuous money flow after 20 years is approximately $614.45.

Answer 2

The future value of a continuous money flow of $175 per year at a 7.5% interest rate compounded continuously for 20 years is approximately $8,123.94.

Step-by-step explanation:

To calculate the amount of a continuous money flow of $175 per year invested at 7.5% compounded continuously for 20 years, we will use the formula for the future value of a continuous money flow, also known as the present value of an annuity due to continuous compounding:

Future Value = P × (e
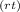`^{(rt)` - 1) / r

Where:

• P is the payment per time period,
• r is the annual interest rate (as a decimal),
• t is the time in years,
• e is the base of the natural logarithm (approximately equal to 2.71828).

Plugging in the numbers:

Future Value = $175 × (e
`^{(0.075`×
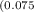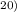`^{20)`) - 1) / 0.075

First, calculate e raised to the power of the product of the interest rate and the time:

e
`^{(0.075`×
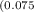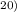`^{20)` ≈ e⁽¹'⁵⁾

Then,

Future Value ≈ $175 × (e⁽¹'⁵⁾ - 1) / 0.075

Now let's calculate the numerical value of e⁽¹'⁵⁾ before finishing our calculation:

e⁽¹'⁵⁾ ≈ 4.48169

Thus,

Future Value ≈ $175 × (4.48169 - 1) / 0.075

Future Value ≈ $175 × 3.48169 / 0.075

Future Value ≈ $175 × 46.4225

Future Value ≈ $8,123.94