a. The potential on the outer surface of the spherical shell is approximately
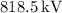 .
.
b. The potential on the surface of the sphere is approximately
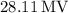 .
.
To solve this problem, you can use the formula for the electric potential
 due to a point charge:
due to a point charge:
![\[ V = (k \cdot |Q|)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/g9e5k7kgnhuxb37udjt5neem61w9khlzdp.png)
where:
-
 is the electric potential,
is the electric potential, -
 is Coulomb's constant
is Coulomb's constant
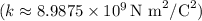 ,
, -
 is the charge, and
is the charge, and -
 is the distance from the charge.
is the distance from the charge.
part a):
a) Potential on the outer surface of the spherical shell:
The charge on the inner surface of the shell induces an equal and opposite charge on the outer surface due to the conductive property of the metal. Therefore, the potential on the outer surface of the shell is due to the charge on the sphere alone.
Given:
- Charge on the sphere,
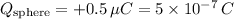
- Radius of the spherical shell,

Using the formula for the potential:
![\[ V_{\text{outer}} = \frac{k \cdot |Q_{\text{sphere}}|}{r_{\text{outer}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8supfe3i1nf60nqi63odfon6uld9e19qns.png)
![\[ V_{\text{outer}} = \frac{8.9875 * 10^9 \, \text{N m}^2/\text{C}^2 * 5 * 10^(-7) \, \text{C}}{5.49 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/cbumbkd8m8duxquogl3ptxv7jb9h870n2z.png)
![\[ V_{\text{outer}} \approx 8.185 * 10^5 \, \text{V} = 818.5 \, \text{kV} \]](https://img.qammunity.org/2024/formulas/physics/high-school/aic3xe3odlj3vou8hbsljj8fa1wtw0v6av.png)
Therefore, the answer is approximately
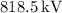 .
.
part b):
b) Potential on the surface of the sphere:
The potential on the surface of the sphere is due to its own charge.
Given:
- Charge on the sphere,
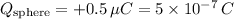
- Radius of the sphere,
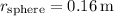
Using the formula for the potential:
![\[ V_{\text{sphere}} = \frac{k \cdot |Q_{\text{sphere}}|}{r_{\text{sphere}}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8tzl2um0x0eco8eeqjx72w0m8dog2ovrpo.png)
![\[ V_{\text{sphere}} = \frac{8.9875 * 10^9 \, \text{N m}^2/\text{C}^2 * 5 * 10^(-7) \, \text{C}}{0.16 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/xjd6kom0v3vy0phx236dwyavbu1yhavhgq.png)
![\[ V_{\text{sphere}} \approx 2.811 * 10^7 \, \text{V} = 28.11 \, \text{MV} \]](https://img.qammunity.org/2024/formulas/physics/high-school/5om0b8aluipsa198pylpqyneeau1d6k1nq.png)
Therefore, the answer is approximately
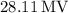 .
.