Question

Find the given higher-order derivative. f(3)(x)=8x7​,f(4)(x)

Answer 1

The fourth derivative, f(4)(x), of the function given that the third derivative is
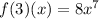`f(3)(x) = 8x^7`, is found using the power rule of differentiation, resulting in
`f(4)(x) = 56x^6.`

Step-by-step explanation:

To find the fourth derivative, f(4)(x), of the function given that the third derivative is f(3)(x) = 8x7, we will apply the power rule for differentiation. The power rule states that the derivative of x to the power of n, denoted as xn, is n multiplied by x to the power of n-1.

Using this rule, we differentiate f(3)(x) = 8x7:

f(4)(x) = d/dx [8x7] = 8 * 7 * x7-1 = 56x6

Therefore, the fourth derivative of the function, f(4)(x), is 56x6.