Question

24 . Does the point (5,10) satisfy the equation: 4y-2x=20

Answer 1

Answer: It does not.

Explanation:

Our task is to determine whether or not the point (5,10) satisfies the equation:
`\sf{4y-2x=20}`.

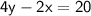Basically, to determine that, we need to plug in 5 (which is the x-coordinate) for x and 10 (which is the y-coordinate) in for y:

`\sf{4(10)-2(5)=20}`

The next step is to simplify.

`\sf{40-10=20}`

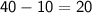
Simplify completely.

`\sf{30=20}`

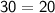
Obviously, this isn't true; we have obtained a false statement, and, therefore, we jump to the conclusion that the point (5,10) does not satisfy the equation 4y - 2x = 20.

Answer 2

No

Explanation:

to determine if (5, 10 ) is a solution, substitute x = 5, y = 10 into the left side of the equation and if equal to the right side then it is a solution.

4y - 2x

= 4(10) - 2(5)

= 40 - 10

= 30 ≠ 20

since left side ≠ right side

then (5, 10 ) is not a solution of the equation