Question

A line has a slope of 5 and passes through the point (12,13). what is the equation of this line?

Answer 1

y = 5x - 47

Given :

• A slope of 5 passing through the point (12,13)

To find :

• Equation of the line

Solution :

We know that,

• equation of a straight line => y = mx + b

ATQ,

• 13 = (5)(12) + b
• 60 + b = 13
• b = 13- 60
• b = -47

Inserting the value of b in the equation,

• y = 5x -47

Therefore,

The equation of the given line would be y = 5x -47

Answer 2

The equation of the line is y = 5x - 47.

Explanation:

The equation of a line with a slope of 5 and passing through the point (12,13) can be found using the point-slope form of linear equations.

The point-slope form is:

`\sf y - y_1 = m(x - x_1)`

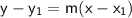
where

• m is the slope,
• (x1, y1) is a point on the line, and
• (x, y) is the point we are solving for.

In this case, m = 5, (x1, y1) = (12, 13), and (x, y) is the unknown point.

Substituting these values into the point-slope form, we get:

`\sf y - 13 = 5(x - 12)`

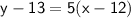
Simplifying the right side of the equation, we get:

`\sf y - 13 = 5x - 60`

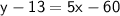
Adding 13 to both sides of the equation, we get the equation of the line in slope-intercept form:

`\sf y = 5x - 60+13`

`\sf y = 5x - 47`

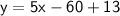
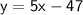
Therefore, the equation of the line is y = 5x - 47.