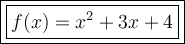Question

Let $f(x)$ be a monic polynomial such that $f(0)=4$ and $f(1)=8$. If $f(x)$ has degree $2$, what is $f(x)$? Enter your answer in the form $ax^2+bx+c$, where $a$, $b$, and $c$ are real numbers.

Answer 1

`f(x)=x^2+3x+4`

Explanation:

A monic polynomial is a type of polynomial in which the coefficient of the highest-degree term (the term with the highest exponent) is equal to one.

Since f(x) is a monic polynomial of degree 2, its general form is f(x) = x² + bx + c, where b and c are real numbers.

Given that f(0) = 4, substitute x = 0 into the function, set it equal to 4 and solve for c:

`\begin{aligned}\textsf{When}\;x=0\implies f(0)=(0)^2+b(0)+c&=4\\0+0+c&=4\\c&=4\end{aligned}`

Given that f(1) = 8, substitute x = 1 into the function, set it equal to 8, substitute the found value of c, and solve for b:

`\begin{aligned}\textsf{When}\;x=1\implies f(1)=(1)^2+b(1)+c&=8\\1+b+c&=8\\1+b+4&=8\\b+5&=8\\b&=3\end{aligned}`

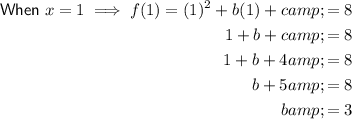
Substitute the found values of b and c into the function:

`f(x)=x^2+3x+4`

Therefore, the monic polynomial of degree 2, where f(0) = 4 and f(1) = 8 is:

`\large\boxed{\boxed{f(x)=x^2+3x+4}}`