Question

Can someone help me please? (i think letter I is wrong since it’s not at the bottom)

solve i through r

Answer 1

`\textsf{E)}\quad 12x+9`

`\textsf{O)}\quad 3x^2+9x-6`

`\textsf{I)}\quad 12x-20`

`\textsf{S)}\quad 4x+7`

`\textsf{D)}\quad 5x+5`

`\textsf{A)}\quad x^2-5x`

`\textsf{E)}\quad 24x^2-15x`

`\textsf{S)}\quad \sf 2x^4+14x^3+8x^2`

`\textsf{Q)}\quad 7x^2`

`\textsf{R)}\quad 116x^2+53x`

`\textsf{W)}\quad 66x^2+40x^2+24x`

`}\textsf{R)}\quad 11x^2-44x`

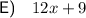
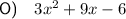
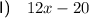
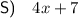
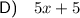
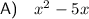
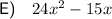
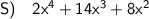
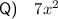
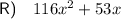
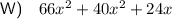
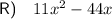
Explanation:

Part 1

The perimeter of a two-dimensional shape is the sum of the lengths of all its outer edges. Therefore, to find the perimeter of each shape, sum the given side lengths.

`\begin{aligned}\textsf{E)}\quad (3x+8)+(4x-1)+(5x+2)&=3x+8+4x-1+5x+2\\&=3x+4x+5x+8-1+2\\&=12x+9\end{aligned}`

`\begin{aligned}\textsf{O)}\quad 2x^2+(9x-10)+x^2+4&=2x^2+9x-10+x^2+4\\&=2x^2+x^2+9x+4-10\\&=3x^2+9x-6\end{aligned}`

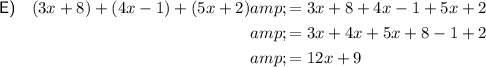
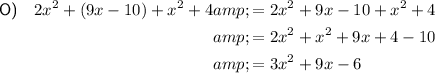
Shape I is a rectangle. The opposite sides of a rectangle are the same length. Therefore, the perimeter of a rectangle is twice the sum of its width and length.

`\begin{aligned}\textsf{I)}\quad 2(2x-3+4x-7)&=2\cdot 2x+2\cdot(-3)+2\cdot4x+2\cdot(-7)\\&=4x-6+8x-14\\&=4x+8x-6-14\\&=12x-20\end{aligned}`

`\hrulefill`

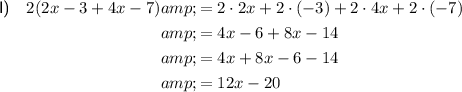
Part 2

The perimeter of a two-dimensional shape is the sum of the lengths of all its outer edges. Therefore, to find the missing side length, subtract the known side lengths from the given perimeter.

`\begin{aligned}\textsf{S)}\quad (13x+11)-(3x-2)-(6x+6)&=13x+11-3x+2-6x-6\\&=13x-3x-6x+11+2-6\\&=4x+7\end{aligned}`

`\begin{aligned}\textsf{D)}\quad (21x+2)-5x-(7x+2)-(4x-5)&=21x+2-5x-7x-2-4x+5\\&=21x-5x-7x-4x+2-2+5\\&=5x+5\end{aligned}`

`\begin{aligned}\textsf{A)}\quad (3x^2-2x-5)-(2x^2-9)-(3x+4)&=3x^2-2x-5-2x^2+9-3x-4\\&=3x^2-2x^2-2x-3x+9-5-4\\&=x^2-5x\end{aligned}`

`\hrulefill`

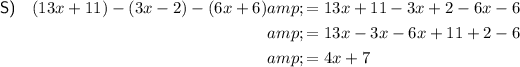
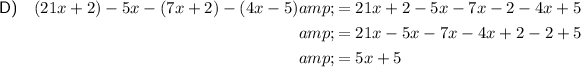
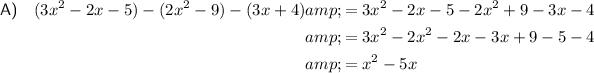
Part 3

To find the area of a rectangle, we can multiply its width by its length.

`\begin{aligned}\textsf{E)}\quad \sf Area&=3x \cdot (8x-5)\\&=3x \cdot 8x + 3x \cdot (-5)\\&=24x^2-15x\end{aligned}`

`\begin{aligned}\textsf{S)}\quad \sf Area&=2x^2 \cdot (x^2+7x+4)\\&=2x^2 \cdot x^2 + 2x^2 \cdot 7x+2x^2 \cdot 4\\&=2x^4+14x^3+8x^2\end{aligned}`

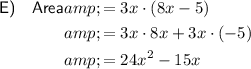
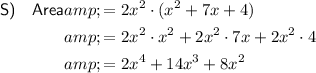
To find the area of shape Q, subtract the area of the cut out square with dimensions
`x * x` from the rectangle with dimensions
`2x * (x+x+2x)`.

`\begin{aligned}\textsf{Q)}\quad \sf Area&=(2x \cdot (x+x+2x))-(x \cdot x)\\&=(2x \cdot 4x)-(x^2)\\&=8x^2-x^2\\&=7x^2\end{aligned}`

`\hrulefill`

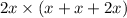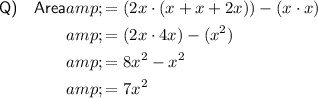
Part 4

To find the areas of the shaded regions, we can subtract the area of the smaller unshaded rectangle from the larger rectangle.

`\begin{aligned}\textsf{R)}\quad \sf Area&=(9x \cdot (16x+5))-(4x \cdot (7x-2))\\&=(9x \cdot 16x + 9x \cdot 5)-(4x \cdot 7x+4x\cdot(-2))\\&=(144x^2+45x)-(28x^2-8x)\\&=144x^2+45x-28x^2+8x\\&=144x^2-28x^2+45x+8x\\&=116x^2+53x\end{aligned}`

`\begin{aligned}\textsf{W)}\quad \sf Area&=(6x^2\cdot (11x+20))-(8 \cdot (10x^2-3x))\\&=(6x^2 \cdot 11x+6x^2 \cdot 20)-(8 \cdot 10x^2+8 \cdot(-3x))\\&=(66x^3+120x^2)-(80x^2-24x)\\&=66x^3+120x^2-80x^2+24x\\&=66x^2+40x^2+24x\end{aligned}`

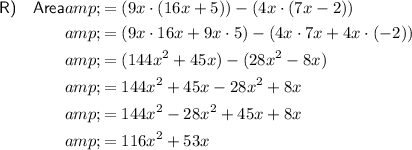
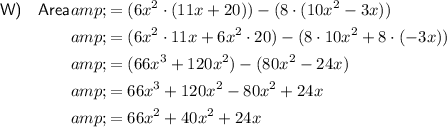
To find the area of the shaded region in shape R, we can subtract the area of the 4 small congruent rectangles from the larger rectangle.

`\begin{aligned}\textsf{R)}\quad \sf Area&=(3x \cdot (5x-12))-(4 \cdot (x \cdot (x+2))\\&=(3x \cdot 5x+3x \cdot (-12))-(4 \cdot (x \cdot x+x \cdot 2))\\&=(15x^2-36x)-(4 \cdot (x^2+2x))\\&=(15x^2-36x)-(4 \cdot x^2+4 \cdot 2x)\\&=(15x^2-36x)-(4 x^2+8x)\\&=15x^2-36x-4x^2-8x\\&=15x^2-4x^2-36x-8x\\&=11x^2-44x\end{aligned}`

`\hrulefill`

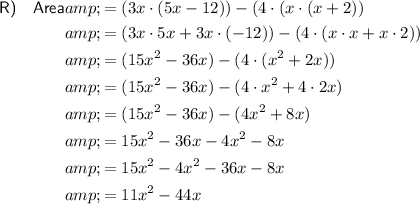
See the attachment for the code.