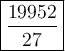Question

Let x, y and z be real numbers such that

\begin{align*} x+y-z &= -8, \\ x-y &= 18,\text{ and} \\ y+z &= 30. \\ \end{align*}
Compute xyz.

Answer 1

`xyz=(19952)/(27)`

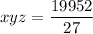
Explanation:

Given system of equations:

`\begin{aligned} x+y-z &= -8 \\ x-y &= 18 \\ y+z &= 30\end{aligned}`

Before we can compute xyz, we first need to find the values of x, y and z. To do this, we must solve the given system of equations.

Rearrange the second and third equations to isolate x and z, respectively:

`\begin{aligned}x-y&=18\\x-y+y&=18+y\\x&=18+y\end{aligned}`
`\begin{aligned}y+z&=30\\y+z-y&=30-y\\z&=30-y\end{aligned}`

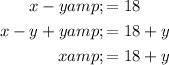
Substitute these into the first equation and solve for y:

`\begin{aligned}x+y-z&=-8\\(18+y)+y-(30-y)&=-8\\18+y+y-30+y&=-8\\3y-12&=-8\\3y&=4\\y&=(4)/(3)\end{aligned}`

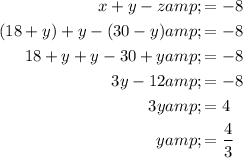
Now, substitute the found value of y into the two rearranged equations to find the values of x and z:

`\begin{aligned}x&=18+(4)/(3)\\\\x&=(54)/(3)+(4)/(3)\\\\x&=(58)/(3)\end{aligned}`
`\begin{aligned}z&=30-(4)/(3)\\\\z&=(90)/(3)-(4)/(3)\\\\z&=(86)/(3)\end{aligned}`

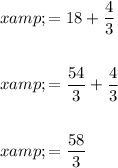
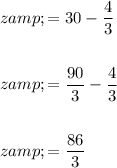
Now we have found the values of x, y and z, we can multiply them to compute xyz:

`\begin{aligned}xyz&=(58)/(3) \cdot (4)/(3)\cdot (86)/(3)\\\\xyz&=(58\cdot4\cdot86)/(3\cdot3\cdot3)\\\\xyz&=(19952)/(27)\end{aligned}`

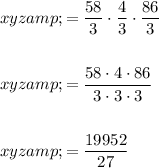
Therefore, the computation of xyz is:

`\large\boxed{(19952)/(27)}`