Question

coco invests 2,000 at the beginning of the year in a fund which credits interest at an annual effective rate of 9%. coco reinvests each interest payment in a separate fund, accumulating at an annual effective rate of 8%. the interest payments from this fund accumulate in a bank account that guarantees an annual effective rate of 7%. determine the sum of the principal and interest at the end of 10 years.

Answer 1

1. First Investment at 9% is 4734.727

2. Reinvested Interest at 8% is 10221.920

3. the sum of the principal and interest at the end of 10 years is approximately $35064.7104.

How did we get the values?

To determine the sum of the principal and interest at the end of 10 years, we need to calculate the future value of each investment separately and then sum them up.

1. First Investment at 9%: The formula for the future value of a single sum is given by:

`\[ FV = PV * (1 + i)^n \]`

where:

- PV is the principal amount (initial investment),

- i is the interest rate per compounding period,

- n is the number of compounding periods.

For the first investment,
`\( PV = $2,000 \), \( i = 0.09 \), and \( n = 10 \)` years.

`\[ FV_1 = 2000 * (1 + 0.09)^(10) \]`

`\[ FV_1 = 2000 * (1.09)^(10) \]`

`\[ FV_1 \approx 4734.727 \]`

2. Reinvested Interest at 8%: For each interest payment, Coco reinvests it at an annual effective rate of 8%. Since interest is compounded annually, the future value after 10 years can be calculated using the same formula:

`\[ FV_2 = (FV_1) * (1 + 0.08)^(10) \]`

`\[ FV_2 \approx 4734.727 * (1.08)^(10) \]`

`\[ FV_2 \approx 10221.920 \]`

3. Interest Payments Accumulated in Bank Account at 7%: The interest payments from the second fund accumulate in a bank account at an annual effective rate of 7%. Again, the future value after 10 years can be calculated:

`\[ FV_3 = (FV_2) * (1 + 0.07)^(10) \]`

`\[ FV_3 \approx 10221.920 * (1.07)^(10) \]`

`\[ FV_3 \approx 20108.0634 \]`

Let us calculate
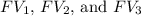`\( FV_1 \), \( FV_2 \), and \( FV_3 \)`, and sum them up to get the total amount at the end of 10 years.

`\[ \text{Total Amount} = FV_1 + FV_2 + FV_3 \]`

`\[ \text{Total Amount} \approx 4734.727 + 10221.920 + 20108.0634 \]`

`\[ \text{Total Amount} \approx 35064.7104 \]`

Therefore, the sum of the principal and interest at the end of 10 years is approximately $35064.7104.