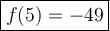Evaluate the function at each specified value of the independent variable and simplify. (If an answer is undefined, enter UNDEFINED.) f(x) = { (x² - 16, 1-2x², x 0 f(x)=. { ( 1 …

Question

asked Nov 6, 2024 156k views

1 Answer

JorgeM · Answer 1 · 2024-11-09T21:22:47+0000

Answer:

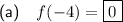
$\textsf{(a)}\quad f(-4)=\boxed{0}$

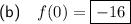
$\textsf{(b)}\quad f(0)=\boxed{-16}$

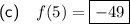
$\textsf{(c)}\quad f(5)=\boxed{-49}$

Explanation:

A piecewise function gives multiple sub-functions for different parts of its domain.

Given piecewise function:

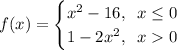
$f(x)=\begin{cases}x^2-16, \;\;x\leq0\\1-2x^2,\;\;x > 0\end{cases}$

Therefore, if x is less than or equal to zero, we should use f(x) = x² - 16.

Similarly, if x is greater than zero, we should use f(x) = 1 - 2x².

$\hrulefill$

To find f(-4), substitute x = -4 into the function.

As -4 ≤ 0, use the first part of the function, f(x) = x² - 16.

$\begin{aligned}f(-4)&=(-4)^2-16\\&=16-16\\&=0\end{aligned}$

Therefore:

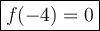
$\large\boxed{f(-4) = 0}$

$\hrulefill$

To find f(0), substitute x = 0 into the function.

As 0 ≤ 0, use the first part of the function, f(x) = x² - 16.

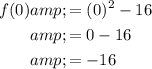
$\begin{aligned}f(0)&=(0)^2-16\\&=0-16\\&=-16\end{aligned}$

Therefore:

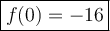
$\large\boxed{f(0) = -16}$

$\hrulefill$

To find f(5), substitute x = 5 into the function.

As 5 > 0, use the second part of the function, f(x) = 1 - 2x².

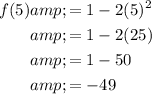
$\begin{aligned}f(5)&=1-2(5)^2\\&=1-2(25)\\&=1-50\\&=-49\end{aligned}$

Therefore:

$\large\boxed{f(5) = -49}$