Question

Glycerol HOCH2CH(OH)CH2OH is a nonvolatile, water-soluble material. Its density is 1.25 g/mL.

Predict the vapor pressure of a solution of 266 mL of glycerol, in 399 mL of water, at the normal boiling point of water.
ATM

Answer 1

The predicted vapor pressure of the solution of 266 mL glycerol and 399 mL water at the normal boiling point of water is approximately
`\(0.8594 \, \text{atm}\).`

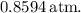
To predict the vapor pressure of the solution, we can use Raoult's law, which states that the vapor pressure of a solution is directly proportional to the mole fraction of each component in the solution.

Given:

- Volume of glycerol = 266 mL

- Volume of water = 399 mL

- Density of glycerol = 1.25 g/mL

First, let's calculate the moles of glycerol and water in the solution:

For glycerol:

`\[ \text{Volume} * \text{Density} = \text{Mass} \]`

`\[ 266 \, \text{mL} * 1.25 \, \text{g/mL} = 332.5 \, \text{g} \]`

The molar mass of glycerol
`(\(C_3H_8O_3\)) is approximately \(92.09 \, \text{g/mol}\).`

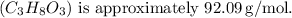
`\[ \text{Moles of glycerol} = \frac{\text{Mass}}{\text{Molar mass}} = \frac{332.5 \, \text{g}}{92.09 \, \text{g/mol}} \approx 3.61 \, \text{mol}\]`

For water:

`\[ \text{Volume} * \text{Density} = \text{Mass} \]`

`\[ 399 \, \text{mL} * 1 \, \text{g/mL} = 399 \, \text{g} \]`

The molar mass of water
`(\(H_2O\)) is approximately \(18.02 \, \text{g/mol}\).`

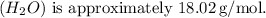
`\[ \text{Moles of water} = \frac{\text{Mass}}{\text{Molar mass}} = \frac{399 \, \text{g}}{18.02 \, \text{g/mol}} \approx 22.17 \, \text{mol}\]`

Now, let's find the mole fraction of each component:

Mole fraction of glycerol:

`\[ \text{Mole fraction} = \frac{\text{Moles of glycerol}}{\text{Total moles in solution}} = \frac{3.61 \, \text{mol}}{3.61 \, \text{mol} + 22.17 \, \text{mol}} \approx 0.1406 \]`

Mole fraction of water:

`\[ \text{Mole fraction} = \frac{\text{Moles of water}}{\text{Total moles in solution}} = \frac{22.17 \, \text{mol}}{3.61 \, \text{mol} + 22.17 \, \text{mol}} \approx 0.8594 \]`

Now, we'll use Raoult's law:

`\[ P_{\text{total}} = P_{\text{glycerol}} * \text{mole fraction of glycerol} + P_{\text{water}} * \text{mole fraction of water} \]`

At the normal boiling point of water, the vapor pressure of pure water is
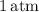`\(1 \, \text{atm}\)` (since it's boiling at its normal boiling point).

So, the vapor pressure of the solution would be:

`\[ P_{\text{total}} = 1 \, \text{atm} * 0.8594 + P_{\text{glycerol}} * 0.1406 \]`

We need to find the vapor pressure of glycerol to calculate
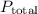`\(P_{\text{total}}\)`. The vapor pressure of glycerol can be considered negligible compared to water at its boiling point. Therefore:

`\[ P_{\text{total}} \approx 1 \, \text{atm} * 0.8594 = 0.8594 \, \text{atm} \]`