HELP help help help help

Question

asked Nov 3, 2024 175k views

2 Answers

Rlafuente · Answer 1 · 2024-11-08T17:15:05+0000

Answer:

3√(2)+9

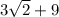
Explanation:

Given expression:

$\frac{6}{\sqrt[4]{2} \cdot √(2)} \cdot \sqrt[4]{2}-(-9)$

To simplify the given expression, follow the order of operations (PEMDAS).

The first fraction is multiplied by ⁴√2. Since the denominator of the fraction contains ⁴√2, we can cancel this common factor:

$\frac{6\cdot \sqrt[4]{2}}{\sqrt[4]{2} \cdot √(2)} -(-9)$

(6)/(√(2)) -(-9)

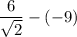
Rationalize the denominator to eliminate the radical from the denominator by multiplying the numerator and denominator by √2:

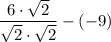
$(6\cdot √(2))/(√(2)\cdot √(2)) -(-9)$

(6√(2))/(2) -(-9)

Carry out the division:

3√(2) -(-9)

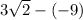
Finally, apply the rule: a - (-b) = a + b

$\large\boxed{\boxed{3√(2)+9}}$