Question

A 200.0g copper wire loses 2350J of heat after it is removed from the electrical grid. What is the change in temperature of this copper wire? (The specific heat of copper is 0.38452 J/g°C)

51.6 0C
60.2 0C
65.0 0C
30.6 0C

Answer 1

The last option, ΔT = 30.6 °C

Step-by-step explanation:

The change in temperature of a 200.0 g copper wire, after losing 2350 J of heat upon being removed from the electrical grid, can be determined using the specific heat of copper.

In this scenario, we're dealing with heat transfer and temperature change in a copper wire. Heat transfer occurs when there is a difference in temperature between an object and its surroundings, leading to the flow of thermal energy. The specific heat of a substance measures how much energy is required to raise the temperature of a unit mass of that substance by one degree Celsius (or Kelvin).

Given that the specific heat of copper is provided as 0.38452 J/g°C, we can use the formula:

`\boxed{\left\begin{array}{ccc}\text{\underline{Heat Transfer Formula:}}\\\\Q=mc\Delta T\\\\\text{Where:}\\\bullet \ Q \ \text{is the heat transferred}\\\bullet \ m \ \text{is the mass}\\\bullet \ c \ \text{is the specific heat}\\\bullet \ \Delta T \ \text{is the change in temperature} \ (T_f-T_i) \end{array}\right}`

In our case, we are given:

• Q = 2350 J
• m = 200.0 g

• c = 0.38452 J/g°C

We want to find:

• ΔT = ?? °C

`\hrulefill`
Start by rearranging the heat formula. Solving for 'ΔT':

`\Longrightarrow Q=mc\Delta T\\\\\\\\\therefore \Delta T=(Q)/(mc)`

Substitute in the given values and calculate 'ΔT':

`\Longrightarrow \Delta T=(Q)/(mc)\\\\\\\\\Longrightarrow \Delta T=(2350 \ J)/((200.0 \ g)(0.38452 \ (J)/(g\textdegree C) ))\\\\\\\\\therefore \boxed{\boxed{T \approx 30.6 \ \textdegree C}}`

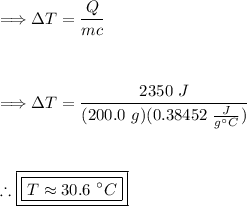
Therefore, the change in temperature of the copper wire is approximately 30.6 °C. Thus, the last option is correct.