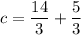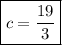Question

Find the largest value of c such that \frac{c^2 + 6c - 27}{c - 3} + 2c = 28.

Answer 1

`c=(19)/(3)`

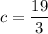
Explanation:

We can solve for the variable
`c` in the equation with the following operations:

`(c^2 + 6c - 27)/(c - 3) + 2c = 28`

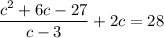
↓ subtracting
`2c` from both sides

`(c^2+6c-27)/(c-3) = 28 - 2c`

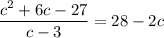
↓ multiplying both sides by
`(c-3)`

`c^2+6c-27 = (28 - 2c)(c-3)`

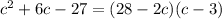
↓ expanding the right side

`c^2+6c-27 = [\,28c + 28(-3)\, ] + [\, (-2c)(c) + (-2c)(-3)\, ]`

↓ combining like terms on the right side

`c^2+6c-27 = -2c^2 + 34c - 84`

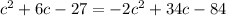
↓ moving all terms to the left side

`3c^2 - 28c + 57 = 0`

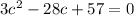
↓ dividing both sides by
`3`

`c^2 - (28)/(3)c + 19 = 0`

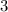
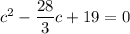
Now, we can complete the square:

↓ subtracting 19 from both sides

`c^2 - (28)/(3)c = -19`

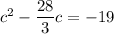
↓ adding
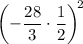`\left(-(28)/(3) \cdot (1)/(2)\right)^(\!2)` to both sides (which simplifies to
`(196)/(9)`)

`c^2 - (28)/(3)c + (196)/(9) = -19 + (196)/(9)`

↓ factoring the left side and combining like terms on the right side

`\left(c - (28)/(3)\cdot (1)/(2)\right)^(\!2) = (25)/(9)`

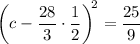
↓ simplifying the second term on the left side

`\left(c - (14)/(3)\right)^(\! 2) = (25)/(9)`

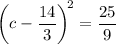
↓ taking the square root of both sides

`\sqrt{\left(c - (14)/(3)\right)^(\! 2)} = \sqrt(25)/(9)`

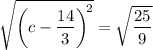
↓ simplifying both sides

`c - (14)/(3) = \pm(5)/(3)`

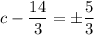
↓ adding
`(14)/(3)` to both sides

`c = (14)/(3) \pm (5)/(3)`

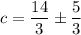
↓ finding the larger value

`c = (14)/(3) + (5)/(3)`

`\boxed{c=(19)/(3)}`