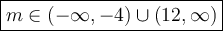Question

Let $m$ be a real number. If the quadratic equation $x^2+mx+4 = 4x - 12$ has two distinct real roots, then what are the possible values of $m$? Express your answer in interval notation.

Answer 1

m ∈ (-∞, -4) ∪ (12, ∞)

Explanation:

Given equation:

`x^2 + mx + 4 = 4x - 12`

To find the possible values of m for which the given equation has two distinct real roots, we need to examine the discriminant of the quadratic equation.

`\boxed{\begin{minipage}{6.8 cm}\underline{Discriminant}\\\\$b^2-4ac$ \quad when $ax^2+bx+c=0$\\\\when $b^2-4ac > 0 \implies$ two real roots.\\when $b^2-4ac=0 \implies$ one real root.\\when $b^2-4ac < 0 \implies$ no real roots.\\\end{minipage}}`

Rearrange the given equation to the standard quadratic form of ax² + bx + c = 0:

`\begin{aligned}x^2 + mx + 4 &= 4x - 12\\\\x^2+mx+4-4x+12&=0\\\\x^2+mx-4x+16&=0\\\\x^2+(m-4)x+16&=0\end{aligned}`

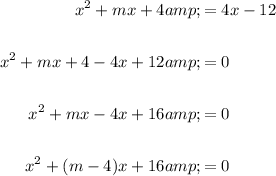
Therefore, the coefficients a, b and c are:

• a = 1
• b = (m - 4)
• c = 16

For a quadratic equation to have two distinct real roots, the discriminant must greater than zero.

Therefore, substitute the values of a, b and c into the discriminant formula, and set it to greater than zero:

`\begin{aligned}b^2-4ac& > 0\\(m-4)^2-4(1)(16)& > 0\\(m-4)^2-64& > 0\\m^2-8m+16-64& > 0\\m^2-8m-48& > 0\end{aligned}`

As the leading coefficient of the quadratic m² - 8m - 48 is positive, its graph is a parabola that opens upwards. Therefore, the values of m that make m² - 8m - 48 positive are the values that are less than the smaller x-intercept and greater than the larger x-intercept, since the part of the graph between the x-intercepts will be below the x-axis and therefore negative.

The x-intercepts are the values of x when y = 0. Therefore, to find the x-intercepts, factor the quadratic m² - 8m - 48, set it to zero, and solve for m:

`\begin{aligned}m^2-8m-48& = 0\\m^2-12m+4m-48& = 0\\m(m-12)+4(m-12)& = 0\\(m+4)(m-12)& = 0\\\\m+4&=0 \implies m=-4\\m-12&=0 \implies m=12\end{aligned}`

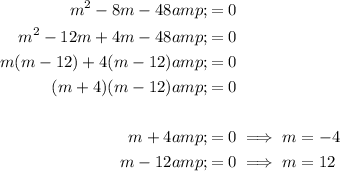
Therefore, the x-intercepts are m = -4 and m = 12.

This means that the discriminant is greater than zero when m < -4 and m > 12.

Therefore, the possible values of m that make the quadratic equation have two distinct real roots are:

`\large\boxed{m \in (-\infty, -4) \cup (12, \infty)}`