Question

The difference between the squares of two numbers is 24 . Four times the square of the first number increased by the square of the second number is 101 . Find the numbers.

Answer 1

Explanation:

Let the numbers be
`x` and
`y`

Given, difference between the squares of two numbers is 24. Assuming |x| > |y|,

`{x}^(2) - {y}^(2) = 24`

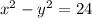
Now the second part of the question: Four times the square of the first number increased by the square of the second number is 101. In equation form,

`4 {x}^(2) + {y}^(2) = 101`

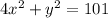
Adding these two equations,

=> x² - y² + 4x² + y² = 125

=> 5x² = 125

=> x² = 25

=> x = ±5

Then y will be,

=> {(+/-5)² - y² = 24)

=> 25 - y² = 24

=> y² = 1

=> y = ± 1

The set of solutions for (x,y) that are possible: (5,1), (5,-1), (-5,1) and (-5,-1).

Note:

The assumption we took earlier |x| > |y| is because square of whether positive or negative values of x and y will always be positive. Hence what matters to us was the numerical value of magnitude of x and y.