Answer:
(1)
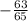
(2) 1.318 rad
Explanation:
1.
π ≤ x ≤ 3π/2 → x at Quadran 3 → x-value negative & y-value negative
3π/2 ≤ y ≤ 2π → y at Quadran 4 → x-value positive & y-value negative
∠x :
sin x = -3/5
y : r = -3 : 5
x = √(r² - y²)
= √(5² - (-3)²)
= -4
x : y : r = -4 : -3 : 5
cos x = -4/5
∠y :
sec y = 13/12
cos y = 12/13
x : r = 12 : 13
y = √(r² - x²)
= √(13² - 12²)
= -5
x : y : r = 12 : -5 : 13
sin y = -5/13
cos(x+y) = cos x · cos - sin x · sin y
=
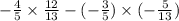
=
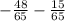
=
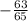
2.
13 - 22cos x - 8sin²x = 0 (assuming incomplete question → the equation = 0)
13 - 22cos x - 8(1 - cos²x) = 0
8cos²x - 22cos x + 5 = 0
(4cos x - 1)(2cos x - 5) = 0
cos x₁ =
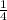
cos x₂ =
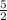 (not valid, as -1 ≤ cos x ≤ 1)
(not valid, as -1 ≤ cos x ≤ 1)
cos x =
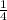
x = 1.318 rad