Question

A rock is thrown straight up from a cliff that is 24 feet above water. If the height

of a rock h, in feet, after t seconds is given by the equation ℎ = -16t^2 + 20t +24, how long will it take for the rock to hit the water?

Answer 1

Rock will take 2 seconds to hit the water.

Explanation:

We need to determine the time at which the height(h) is equal to 0 since the rock will hit the water when its height is 0.

Given the equation for the height{h) of the rock:

`\sf h = -16t^2 + 20t + 24`

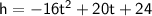
We set height h to 0 and solve for time t.

`\sf 0 = -16t^2 + 20t + 24`

Now, we have a quadratic equation. To solve it, we can use the quadratic formula:

`\sf t = (-b \pm √(b^2 - 4ac))/(2a)`

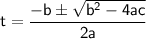
In this case, the coefficients are a = -16, b = 20, and c = 24.

Substituting these values into the quadratic formula:

`\sf t = (-20 \pm √(20^2 - 4 \cdot (-16) \cdot 24))/(2 \cdot (-16))`

`\sf t = (-20 \pm √(400 + 1536))/(-32)`

`\sf t = (-20 \pm √(1936))/(-32)`

`\sf t = (-20 \pm 44)/(-32)`

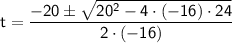
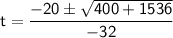
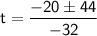
So, we have two possible solutions for time(t).

`\sf t = (-20 + 44)/(-32) = (24)/(-32) = -0.75`

`\sf t = (-20 - 44)/(-32) = (-64)/(-32) = 2`

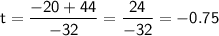
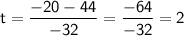
We discard the negative solution because time cannot be negative in this context.

Therefore, the rock will hit the water after approximately 2 seconds.