Question

Write the equation of the parabola in vertex form. Vertex (3,1), point (2, -4)

Answer 1

`\[y = -5(x - 3)^2 + 1\]\\y=-5x^2+30x-44`

Explanation:

The vertex form of a parabola is given by:

`\[y = a(x - h)^2 + k\]`

where (h, k) is the vertex of the parabola. Given that the vertex is (3, 1), we have h = 3 and k = 1. Now we need to find the value of 'a'. To do that, we can use the point (2, -4) that lies on the parabola.

Substitute the values into the equation:

`\[-4 = a(2 - 3)^2 + 1\]`

Simplify:

`-4 = a(-1)^2 + 1\\\-4 = a + 1`

Solve for 'a':

`a = -4 - 1\\a = -5`

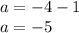
Now that we have 'a', the equation of the parabola in vertex form is:

`\[y = -5(x - 3)^2 + 1\]`

Answer 2

y=−5(x−3)

2

+1

Explanation: