1 Answer

Ben Clifford · Answer 1 · 2024-04-23T15:51:34+0000

$\Large{\boxed{\sf Value \ of \ a = (7)/(2) = 3.5}}$

$\\$

If a point lies on a line, then its coordinates satisfy the equation of said line.

$\\$

Given linear equation:

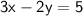
$\sf 3x - 2y = 5$

$\\$

First, substitute the coordinates of the points into the equation:

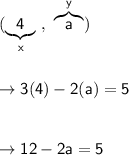
$\sf (\underbrace{\sf 4}_(\sf x) \ , \ \overbrace{\sf a}^(y)) \\ \\ \\ \rightarrow \sf 3(4) - 2(a) = 5 \\ \\ \\ \rightarrow \sf 12 - 2a = 5$

$\\$

Now, solve for a.

Move the constants to the right side of the equation by subtracting 12 from both sides:

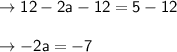
$\rightarrow \sf 12 - 2a - 12 = 5 - 12 \\ \\ \rightarrow \sf -2a = -7$

$\\ \\$

Finally, divide both sides of the equation by -2:

$\rightarrow \sf (-2a)/(-2) = (-7)/(-2) \\ \\ \\ \rightarrow \boxed{\boxed{\sf a = (7)/(2) = 3.5}}$

Please log in or register to add a comment.