Question

Which statement best compares momentum and kinetic energy? A. If you double the velocity of an object, its kinetic energy doubles. But for the same increase in velocity, the momentum increases four times. B. If you double the velocity of an object, its momentum doubles. But for the same increase in velocity, the kinetic energy increases four times. C. If you double the velocity of an object, its momentum and kinetic energy doubles. D. If you double the velocity of an object, its momentum and kinetic energy increases four times.

Answer 1

Option B best compares momentum and kinetic energy. If you double the velocity of an object, its momentum doubles. But for the same increase in velocity, the kinetic energy increases four times.

Step-by-step explanation:

Momentum is a measure of an object's motion and is defined as the product of its mass and velocity. Mathematically, momentum (p) is given by the equation:

`\boxed{\left\begin{array}{ccc}\text{\underline{Momentum:}}\\\\\vec P=m\vec v\\\\\text{Where:}\\\bullet \ \vec P \ \text{is the momentum}\\\bullet \ m \ \text{represents the mass of the object}\\\bullet \ \vec v \ \text{represents the object's velocity}\end{array}\right}`

Kinetic energy is the energy an object possesses due to its motion. It depends on both the mass and velocity of the object. The formula for kinetic energy (K) is:

`\boxed{\left\begin{array}{ccc}\text{\underline{Kinetic Energy:}}\\\\ K = (1)/(2)mv^2 \\\\\text{Where:}\\\bullet \ K \ \text{is the kinetic energy}\\\bullet \ m \ \text{is the mass of the object}\\\bullet \ v \ \text{is the velocity of the object}\end{array}\right}`

`\hrulefill`
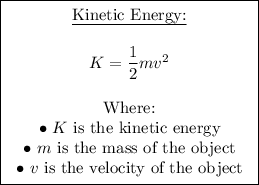
Now, let's break down the comparison between momentum and kinetic energy as presented in the options:
`\hrulefill`
Option A: This option states that if you double the velocity of an object, its kinetic energy doubles. This is correct according to the kinetic energy formula. However, it also says that for the same increase in velocity, the momentum increases four times. This is incorrect. The correct relationship between momentum and velocity is linear (directly proportional), not quadratic. When velocity doubles, momentum doubles as well.

Option B: This is the correct option. It accurately describes the relationship between momentum and velocity. Doubling the velocity doubles the momentum, and the kinetic energy increases by a factor of four when velocity is doubled.

Option C: This option is incorrect. Doubling the velocity would indeed double both momentum and kinetic energy, but it does not accurately represent the relative increase in kinetic energy with respect to the increase in momentum.

Option D: This option is incorrect. Doubling the velocity does not result in momentum and kinetic energy both increasing by a factor of four. This statement does not accurately reflect the principles of momentum and kinetic energy.

In summary, Option B provides the most accurate comparison between momentum and kinetic energy.

`\hrulefill`

We can prove that this statement is accurate mathematically:

Now, let's consider an initial state where an object has mass, 'm,' and velocity, 'v.' The initial momentum (P₁) and initial kinetic energy (K₁) of the object are given by:

`\bullet \ P_1=mv\\\\\\\bullet \ K_1=(1)/(2)mv^2`

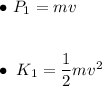
If the velocity of the object is doubled to 2v, the new momentum (P₂) and new kinetic energy (K₂) become:

`\bullet \ P_2=m(2v)\\\\\Longrightarrow P_2=2mv \\\\\therefore \boxed{\boxed{P_2=2P_1}}\\\\\\\bullet \ K_2=(1)/(2)m(2v)^2\\\\ \Longrightarrow K_2=(1)/(2)m(2^2)(v^2)\\\\\Longrightarrow K_2= 4 \cdot (1)/(2)mv^2 \\\\\therefore \boxed{\boxed{K_2=4K_1}}`

Thus, we have proven the statement is accurate mathematically.