Question

The given rectangle and square have the same perimeter. The breadth of the rectangle is one-third of the length of the side of the square. The length of the rectangle is:

Answer 1

Let's denote the side length of the square as "s" and the breadth of the rectangle as "b." According to the given information, the perimeter of the square is 4s and the perimeter of the rectangle is 2(length + breadth).

Since the breadth of the rectangle is one-third of the length of the side of the square, we have:

b = (1/3)s

The perimeter of the rectangle can be expressed as:

2(length + breadth) = 2(length + (1/3)s)

Since the perimeters of the square and the rectangle are equal:

4s = 2(length + (1/3)s)

Simplify the equation:

4s = 2length + (2/3)s

Now, isolate the length term:

2length = 4s - (2/3)s
2length = (12/3)s - (2/3)s
2length = (10/3)s

Divide both sides by 2:

length = (5/3)s

So, the length of the rectangle is (5/3) times the side length of the square.

Answer 2

`\sf \textsf{ Length of rectangle }= \sf (5)/(3) \textsf{ times of sqaure}`

Explanation:

Let's denote:

• The length of the rectangle is L.
• The breadth of the rectangle is B.
• The side length of the square is S.

Given that the breadth of the rectangle is one-third of the length of the side of the square, we can write:

`\sf B = (S)/(3)`

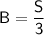
The perimeter of a rectangle is given by:

`\sf P_{\text{rectangle}} = 2L + 2B`

The perimeter of a square is given by:

`\sf P_{\text{square}} = 4S`

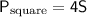
Given that the rectangle and square have the same perimeter:

`\sf 2L + 2B = 4S`

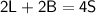
Substitute the value of B from the given relationship:

`\sf 2L + 2\left((S)/(3)\right) = 4S`

Now, solve for L.

`\sf 2L + (2S)/(3)= 4S`

`\sf 2L = 4S - (2S)/(3)`

`\sf 2L = (12 S - 2S)/(3)`

`\sf 2L = (10S)/(3)`

`\sf2L = (10S)/(3* 2)`

`\sf L = (5)/(3) * S`

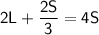
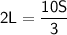
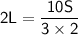
So, the length of the rectangle L is
`\sf (5)/(3)` times the side length of the square S.