Question

Chapter 4; The Laws of Morion 17A*70.0-kilogram man jumps 1.00m down onto a concrete walkway. His downward motion stops in 0.0200second If he forgets to bend his knees, what force is transmitted to his leg bones?

Answer 1

Approximately
`1.62 * 10^(4)\; {\rm N}`, assuming that
`g = 9.81\; {\rm N\cdot kg^(-1)}`.

Step-by-step explanation:

The average normal force from the ground on this person during the impact can be found in the following steps:

• Find the initial gravitational potential energy of this person before the jump.
• Using the conservation of mechanical energy, derive the speed of the person right before landing.
• From the change in velocity, derive the average acceleration during the impact.
• From acceleration, derive the average net force during the impact.
• Find the normal force from the ground using the fact that the net force on this person is the combined result of weight and normal force.

At a height of
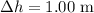`\Delta h = 1.00\; {\rm m}` above the ground, the gravitational potential energy (
`\text{GPE}`) of this
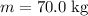`m = 70.0\; {\rm kg}` person would be:

`\begin{aligned} (\text{GPE, initial}) &= m\, g\, \Delta h \end{aligned}`.

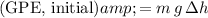Right before landing, the
`\text{GPE}` of this person would be approximately
`0`. By the conservation of mechanical energy, these energy would have been entirely converted into the kinetic energy (
`\text{KE}`) of this person.

In other words:

`(\text{KE, final}) = (\text{GPE, initial}) = m\, g\, \Delta h`.

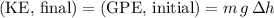When object of mass
`m` travels at a speed of
`v`, the
`\text{KE}` of that object would be
`(1/2)\, m\, v^(2)`. Thus, if this person is travelling at a speed of
`v\!` right before landing:

`\displaystyle (\text{KE, final}) = (1)/(2)\, m\, v^(2)`.

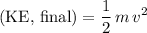Equate the two expressions for the kinetic energy right before landing to obtain:

`\displaystyle (1)/(2)\, m\, v^(2) = m\, g\, \Delta h`.

`\begin{aligned}v &= √(2\, g\, \Delta h)\end{aligned}`.

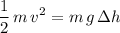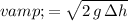In other words, this person would be travelling at a speed of
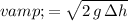`\begin{aligned}v &= √(2\, g\, \Delta h)\end{aligned}` right before landing (
`\Delta h = 1.00\; {\rm m}`.)

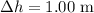During the
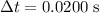`\Delta t = 0.0200\; {\rm s}` of impact, the velocity of this person changed from
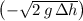`\left(-√(2\, g\, \Delta h)\right)` (negative since this person was initially travelling downward) to
`0`. The change in velocity would be
`\Delta v = 0 - \left(-√(2\, g\, \Delta h)\right) = √(2\, g\, \Delta h)`.

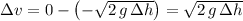Divide the change in velocity by duration to find the average acceleration:

`\begin{aligned}a &= (\Delta v)/(\Delta t) = (√(2\, g\, \Delta h))/(\Delta t)\end{aligned}`.

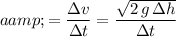Multiply the average acceleration by mass to find the average net force:

`\begin{aligned}F_{\text{net}} &= m\, a \\ &= (m\, √(2\, g\, \Delta h))/(\Delta t)\end{aligned}`.

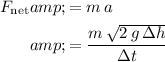The net force on this person is the combined effect of weight
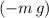`(-m\, g)` (negative because this force points downward) and the normal force from the ground:

`F_{\text{net}} = (\text{weight}) + (\text{normal force})`.

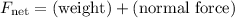Rearrange this equation to find the normal force from the ground:

`\begin{aligned} & (\text{normal force}) \\ &= F_{\text{net}} - (\text{weight}) \\ &= (m\, √(2\, g\, \Delta h))/(\Delta t) - (-m\, g) \\ &= (m\, √(2\, g\, \Delta h))/(\Delta t) + m\, g \\ &= m\, \left((√(2\, g\, \Delta h))/(\Delta t) + g\right) \\ &= (70.0)\, \left((√(2\, (9.81)\, (1.00)))/(0.0200) + 9.81\right)\; {\rm N} \\ &\approx 1.62 * 10^(4)\; {\rm N}\end{aligned}`.

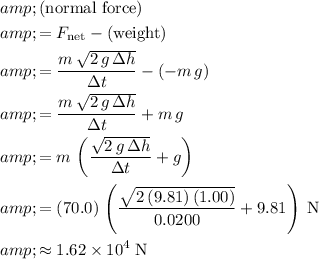In other words, the ground would exert a normal force of approximately
`1.62 * 10^(4)\; {\rm N}` on this person during the impact.