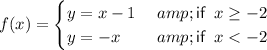Question

PLEAZE HELP PICTURE BELOW!!!

Answer 1

`f(x)=\begin{cases} y=x-1\;&\textsf{if}\;\;x \geq -2\\y=-x\;&\textsf{if}\;\;x < -2\end{cases}`

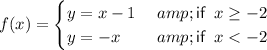
Explanation:

The given graph is the graph of a piecewise function.

A piecewise function is a combination of various graphs, each reflecting the behavior of the function on a distinct interval.

The given graph has two straight lines:

• Line 1 (positive slope) has a closed circle at the endpoint (-2, -3), and continues indefinitely in the upper-right direction after passing through point (3, 2).
• Line 2 (negative slope) has an open circle at the endpoint (-2, 2), and continues indefinitely in the upper-left direction after passing through point (-5, 5).

To write the piecewise function, we need to find the equations of the two lines by finding their slopes, then substituting the slopes and one of the points into the point-slope form of a linear equation.

`\boxed{\begin{minipage}{8cm}\underline{Slope Formula}\\\\Slope $(m)=(y_2-y_1)/(x_2-x_1)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.\\\end{minipage}}`

`\boxed{\begin{minipage}{5.8 cm}\underline{Point-slope form of a linear equation}\\\\$y-y_1=m(x-x_1)$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $(x_1,y_1)$ is a point on the line.\\\end{minipage}}`

Line 1

To find the slope (m) of line 1, substitute the endpoint (-2, -3) and the point on the line (3, 2) into the slope formula:

`m=(2-(-3))/(3-(-2))=(5)/(5)=1`

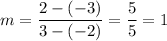
Now, substitute the found slope and one of the points into the slope-point formula:

`\begin{aligned}y-(-3)&=1(x-(-2))\\y+3&=x+2\\y+3-3&=x+2-3\\y&=x-1\end{aligned}`

Therefore, the equation of line 1 is:

`\large\boxed{y=x-1}`

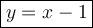
As there is a closed circle at endpoint (-2, -3), the value of x = -2 is included in the interval for this piece of the function. Therefore, the interval for y = x - 1 is x ≥ -2.

Line 2

To find the slope (m) of line 2, substitute the endpoint (-2, 2) and the point on the line (-5, 5) into the slope formula:

`m=(5-2)/(-5-(-2))=(3)/(-3)=-1`

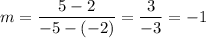
Now, substitute the found slope and one of the points into the slope-point formula:

`\begin{aligned}y-2&=-1(x-(-2))\\y-2&=-x-2\\y-2+2&=-x-2+2\\y&=-x\end{aligned}`

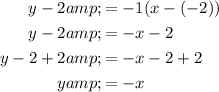
Therefore, the equation of line 2 is:

`\large\boxed{y=-x}`

As there is an open circle at endpoint (-2, 2), the value of x = -2 is not included in the interval for this piece of the function. Therefore, the interval for y = -x is x < -2.

Solution

Therefore, the piecewise function for the given graph is:

`f(x)=\begin{cases} y=x-1\;&\textsf{if}\;\;x \geq -2\\y=-x\;&\textsf{if}\;\;x < -2\end{cases}`